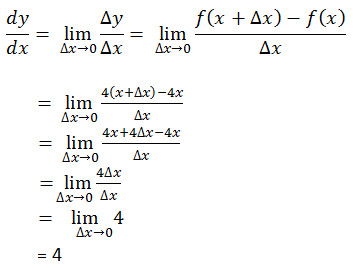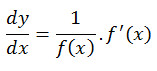Rumus Turunan (diferensial)
Matematika
Apa sih
Turunan?
Definisi turunan aga susah
kalau di berikan dalam bentuk kata (verbal). Sobat bisa misalkan ada y yang
merupakan fungssi dari x, ditulis y = f(x). Yang dimaksud dengan turun y
terhadap x (dinotasikan dy/dx) atau sering ditulis y’ (baca : “y aksen”)
didefinisikan sebagai

masih bingung? kita simak contoh berikut
sobat punya persamaan y = 4x maka nilai dari turunan tersebut menurut definisi
di atas adalah
Rumus –
Rumus Turunan Fungsi Matematika
Buat memudahkan sobat belajar
berikut rumushitung.com rangkumkan berbagai rumus turuna. Check this out.. 
Rumus 1 : Jika y = cxn dengan c dan n
konstanta real , maka dy/dx = cn xn-1
contoh
y = 2x4 maka dy/dx = 4.2x4-1
= 8x3
kadang ada soal yang pakai pangkat pecahan atau akar
y = 2√x = 2x1/2 turunannya adalah 1/2.2 x (1/2-1) = x -1/2
= 1/√x
Rumus 2 : Jika y = c dengan c adalah konstanta maka dy/dx
= 0
contoh jika y = 6 maka turunannya adalah sama dengan nol (0)
Rumus 3 : Jika y = f(x) + g(x)
maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh
y = x3 + 2x2 maka y’ = 3x2
+ 4x
y = 2x5 + 6 maka y’ = 10x4 + 0 = 10x4
Rumus 4 : Turunan Perkalian
Fungsi Jika y f(x).g(x) maka y’ = f'(x) . g(x) + g'(x) . f(x)
contoh
y = x2 (x2+2) maka
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3 + 4x (jawaban ini juga bisa sobat peroleh dengan mengalikan
terlebih dahulu lalu menggunakan rumus 3)
Rumus 5 : Turunan Pembagian Fungsi
contoh
soalnya
Rumus 6 : jika sobat punya y =
[f(x)]n maka turunannya adalah n [f(x)]n-1
. f'(x)
contoh
Rumus 7 : Turunan Logaritma
Natural misal y = ln f(x) maka turunannya
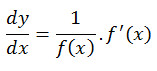 contoh soal
contoh soal
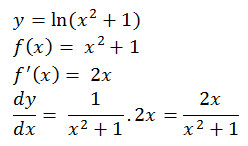
Rumus 8 : ef(x) maka dy/dx = ef(x).f'(x)
contoh :
y = e2x+1
f(x) = 2x+1
f'(x) = 2
maka f’ = e2x+1 . 2 = 2e2x+1
Rumus 9 : Turunan Trigonometri
Sin
Jika sobat punya y = sin f(x) maka turunannya adalah y’ =
cos f(x) . f'(x)
contoh :
y = sin(x2 + 1) maka
y’ = cos (x2 +1) . 2x = 2x. cos (x2 +1)
Rumus 10 :
Turunan Trigonometri Cos
Jika sobat punya y = cos f(x)
maka turunanya adalah y’ = -sin f(x). f'(x)
contoh :
y = cos (2x+1) maka turunannya
y’ = -sin (2x+1) . 2 = -2 sin (2x+1)
Rumus Turunan Kedua
rumus turunan kedua sama dengan turunan dari turunan pertama (sobat turunkan
sebanyak dua kali). Turunan kedua sobat peroleh dengan menurunkan turunan
pertama. Contoh :
Turunan kedua dari x3 + 4x2
turunan pertama = 3x2 + 8x
turunan kedua = 6x + 8

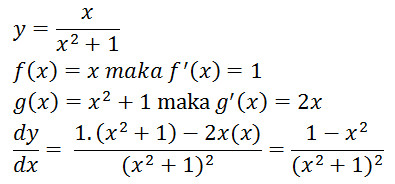
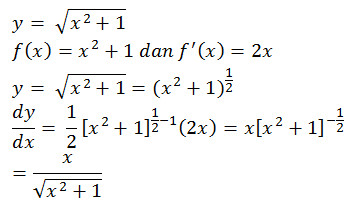
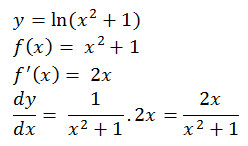
 RSS Feed
RSS Feed Twitter
Twitter




 20.51
20.51
 elisriwahyuni
elisriwahyuni